It’s time to solve another Riddler. This one’s not a war, but a geometry puzzle instead. The problem statement this time is pretty succinct, so I’ll reproduce it in full here:
What whole number dimensions can rectangular prisms have so that their volume (in cubic units) is the same as their surface area (in square units)?
So, what’s that mean? Well, a rectangular prism is just a box. Really – like an Amazon box. It has a length, width, and height and you can calculate its volume and surface area pretty easily as follows:
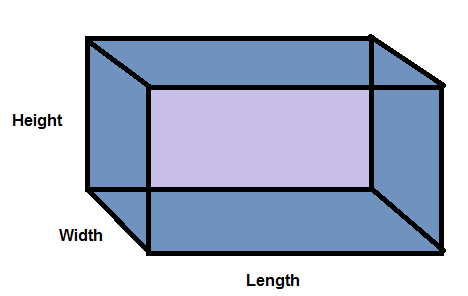
So we’re interested in whole number solutions for length, width, and height, where the two formulas above are equal. It’s probably possible to come up with a nice mathematical solution, but we’re going to take a different route. We’ll solve it with a one-liner:
A prism is a place for light waves who commit minor refractions
🤦
No, not that kind of one-liner. And I am sorry about that. Really…sorry. No, I’m talking about one* line of code. That’s right, this problem can be solved with one* line of code. I’ll get straight to it:
from itertools import combinations_with_replacement as c
[print((L,W,H)) for (L,W,H) in c(range(1, 100), 3) if L*W*H == 2*(L*W+W*H+H*L)]
* Yes, I do understand that this is technically two lines of code – please give me a break for the import statement
That’s it! And this is not a 1,000 character obfuscated nightmare. It fits neatly into 80 characters and it’s actually quite decipherable. So, what is this sorcery? Well, it’s python, of course. Here’s the breakdown:
for (L,W,H) in c(range(1, 100), 3) – generates all values of length, width, and height from (1,1,1) to (100,100,100)
if L*W*H == 2*(L*W+W*H+H*L) – makes sure that the volume equals the surface area
print((L,W,H)) – displays the solutions
And speaking of the solutions, here they are:
(3, 7, 42)
(3, 8, 24)
(3, 9, 18)
(3, 10, 15)
(3, 12, 12)
(4, 5, 20)
(4, 6, 12)
(4, 8, 8)
(5, 5, 10)
(6, 6, 6)
Would you like to see a picture of that? Sure thing – I love pictures! And you can have that for the low cost of just two more* lines of code:
from itertools import combinations_with_replacement as c
p = [(L,W,H) for (L,W,H) in c(range(1, 100), 3) if L*W*H == 2*(L*W+W*H+H*L)]
import mpl_toolkits.mplot3d, matplotlib.pyplot as m
m.figure().add_subplot(111, projection='3d').scatter(*zip(*p))
m.show()
* I know – it’s three!
Here’s the result:
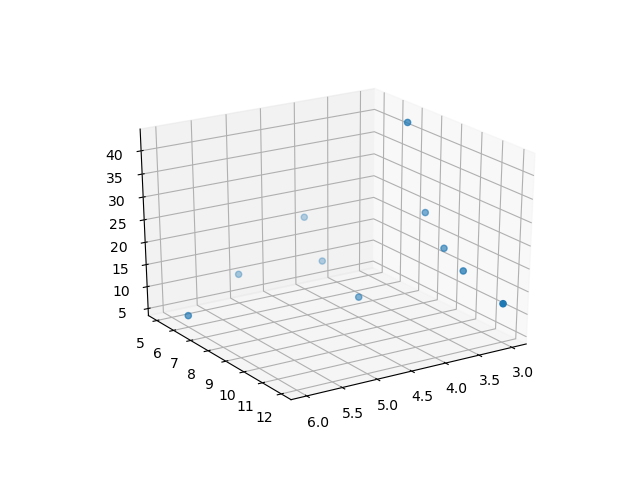
If you squint, you can almost see a pattern emerging, so it’s natural to wonder what might happen if you allow sizes larger than 100. As it turns out, that is pretty hard for a 2017 laptop to do. It doesn’t produce much either. Checking the first 100 values of length, width, and height takes about ten milliseconds, but at the time of this writing, my computer has spent about 10 hours checking the next 54 billion possibilities, without a single hit, so I think we’ve probably found all we can find. And while you think on that, here are some more pretty pictures. First, here’s what all possible solutions (not just whole number solutions) to the problem look like. It doesn’t really matter which axis represents length or width or height because it’s all symmetrical:
And here’s that same graph, scaled down to the range containing the points we found. Sorry for the ugly plot labels – I’m not a very good with visualization:
I had actually expected an infinite number of solutions, so it’s interesting that there are so few of them and that they all fall within a very small range. Can you prove or disprove this? What do you think?