Jocks vs. Nerds

Each Contestant Meets All Other Contestants In Turn

A few years ago, a co-worker participated in a local cricket league. Each team played all of the others in the league twice, and the top few qualified for a playoff. He wanted to know how many games his team needed to win in order to guarantee an appearance in the playoffs. This type of scheduling goes by the name “round-robin”.

I was interested in the following questions:

1. In the worst case, how many wins would a team need in order to advance? This is the case my colleague asked about.
2. In the best case, how few wins could a team achieve and still make the playoffs?
3. What is the average case? How many wins would be necessary to make the playoffs 50% of the time?

I don’t remember the specifics of my colleague’s tournament, so let’s just solve the problem in general.

Average Case

Taking these questions in reverse order, let’s start with number 3. As it turns out, I wasn’t curious enough to figure it out, so it remains unanswered (at least to me). Perhaps I’ll revisit it someday. Problem solved! On to number 2.

Game Over Nerds Win (Best Case)

Another way to describe this is something like the luckiest case. How abysmally can your team perform and still mathematically make it to the playoffs? I’ll assume that it’s possible for two teams to have the same record, while one advances and the other does not (this is usually the case when there is no time for another game, e.g., the sixth and final tie-breaking condition for the Big East NCAA basketball conference championship is just a coin flip).

In this scenario, there must be two groups of teams, the jock teams and the nerd teams (and, you guessed it, your team is a nerd team). The jock teams always beat the nerd teams, and the jocks occupy all but one of the qualifying spots, leaving all of the nerds to fight for the last one. Let’s call   the total number of competitors and the number of qualifiers. Then there are jocks and nerds. If each of the nerds splits their matches with all of the others, there will be a tie between all of them, resulting in one team advancing with a tie-breaker (coin flip). This means each nerd team wins games, and this is the lowest win total possible to still advance. You can’t give up any more wins to the jocks, so If you went any lower, one of the other nerds would have at least one more win than you, and you wouldn’t qualify.

Jocks Lose (Worst Case)

The worst case is actually the question I was asked, and it represents the nightmare scenario – where your team performs exceptionally, but still fails to advance on the tie-breaker. Let’s call up the jocks and nerds again. This time there are more jocks than qualifying spots, by one. The jocks still beat all of the nerds twice, then they split their remaining games against each other, for an additional wins each. This gives each jock team a total of wins. But even if you are one of the jocks, you could still lose the tie-breaker! So we need one more win – that is, , to guarantee that we advance.

What Does It Look Like?

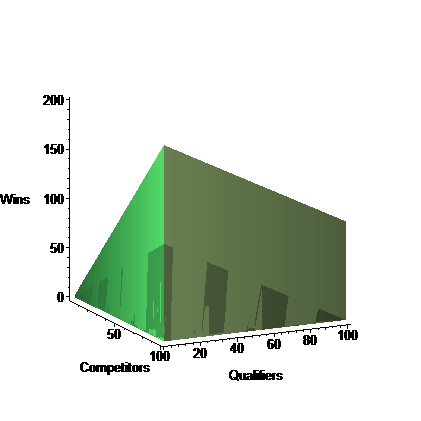
Well, I don’t have any cool artwork for this one, so I thought it might be fun to at least see what these functions look like on a 3D graph. With old friend Maple 8 (yes, the one from 2002), it’s pretty easy to generate a 3D plot with both functions in Q and C. In the image below, the worst case is represented by the “top” of the structure, and the best (luckiest) case is represented by the strange-looking shaded region.

You can see that as the number of qualifiers shrinks relative to the number of competitors, the required win total really skyrockets. For example, if just two out of five teams qualify, six wins would not be enough to guarantee a playoff spot.

I don’t have much else to say about this, except that I think this is one reason why data nerds really love baseball – there are so many games that there are few surprises, and even ties are broken with yet another game, instead of some random device. Statisticians hate small sample sizes, and a single or double match round-robin, while theoretically fair for all participants,  just doesn’t provide enough data for a statistically significant result.